문제 설명
여러 사각형의 겉면을 따라 목표지점으로 갈 수 있는 최단 거리를 구하는 문제이다.
주의 사항
단순 선을 격자의 칸으로 생각하고 최단거리를 탐색하게 되면 이슈가 있을 것이다.
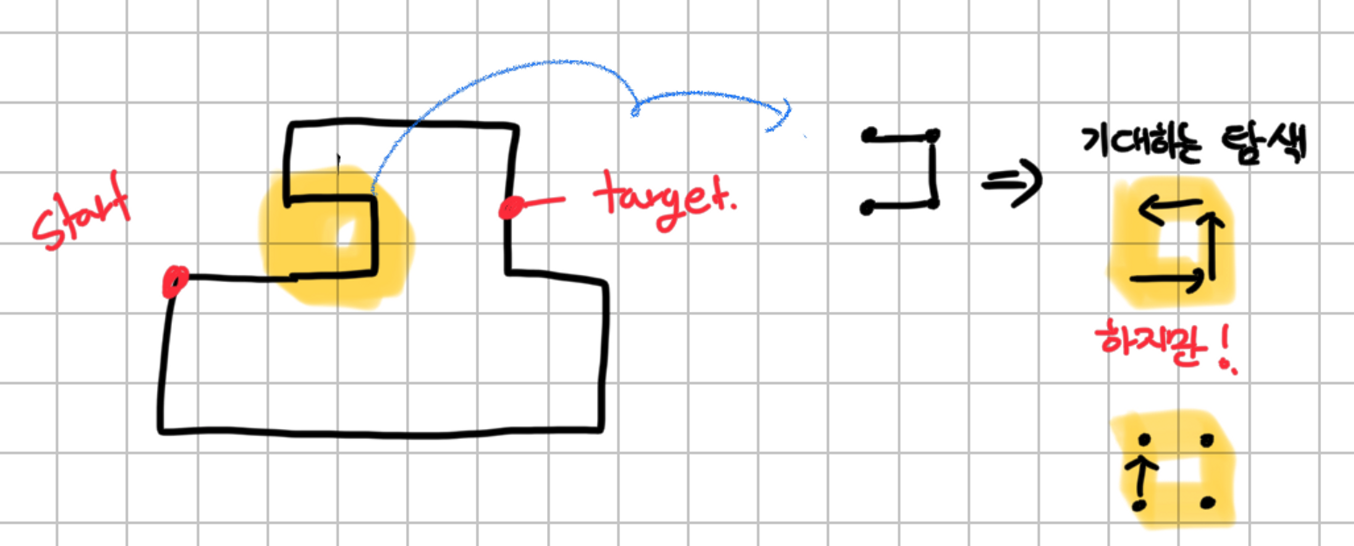
왼쪽 그림 처럼 겉면이 표시된 경우를 보면 우리가 기대하는 탐색과는 다르게 탐색을 하게 된다.
왜냐하면 4방향을 탐색하면서 갈 수 있는지 판단할 것이기 때문이다.
2배율로 격자판을 확장하면 저런 경우를 방지할 수 있다!

기대하는 바와 다르게 탐색 하는 경우를 방지하기 위해 2배율을 한다면 이런식으로 좌표도 확장 되어 거리가 생기니 기대하는 탐색과 다르게 탐색 되지 않게된다!

또다른 시도로는 각 칸에 갈수 있는 방향을 넣어줬다.(정사각형의 입력을 주어질때)
하지만 해당 방법에서 위 그림의 경우 예외를 방지할 수 있지만 또다른 예외가 발생한다.
테스트 케이스 5번을 보면 이런 예외가 발생한다.
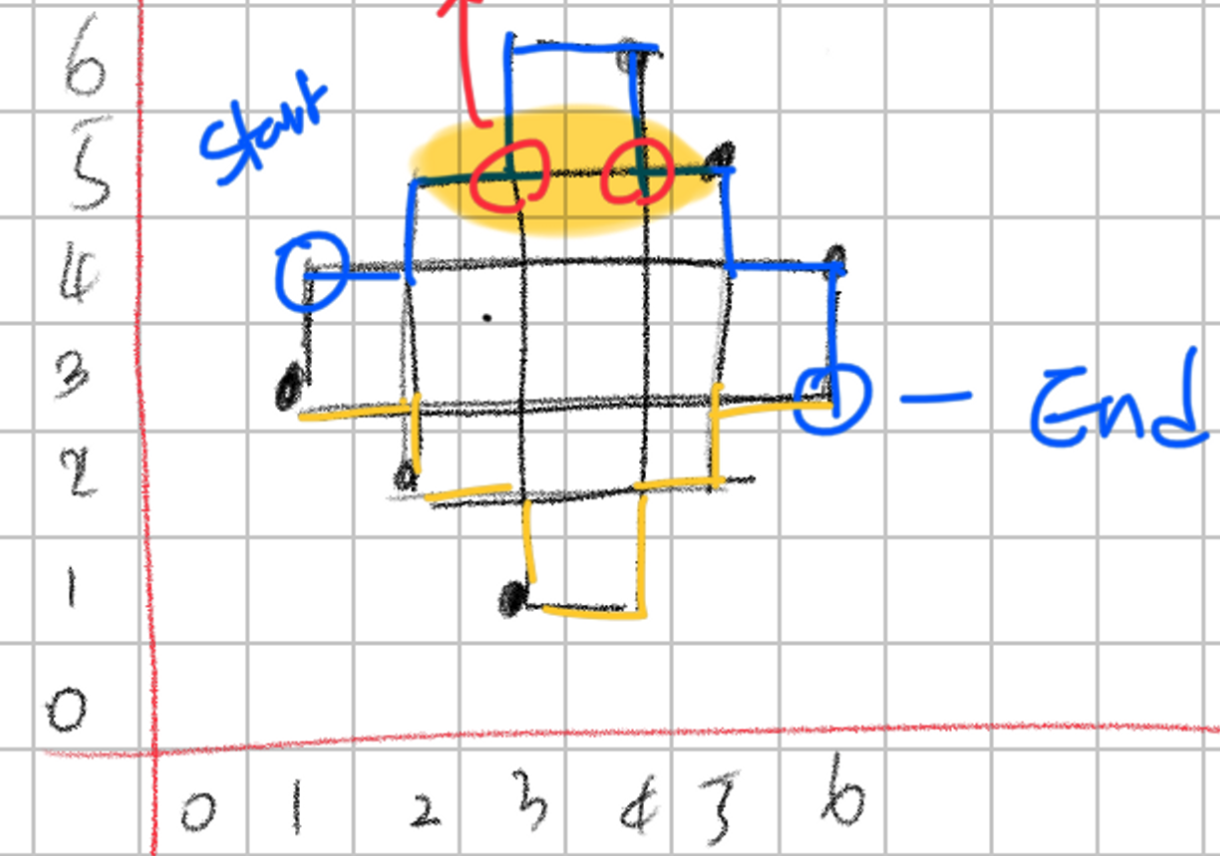
노랑 격자칸은 오른쪽 왼쪽 위쪽도 갈 수 있다. 그래서 해당 직사각형이 촘촘하게 형성된 경우는 사각형 내부에도 포함이 되지 않을 뿐더러 예외를 잡을 수 없었다….
방향에 우선순위도 고려해봤지만… 결국 짧은 탐색이라 먼저 return 하게 된다..
촘촘한 사각형인 경우는 방향을 넣어주는 방법은 예외를 피해 갈 수 없다.. 이런 부분은 하드 코딩으로 막아줘야 하는데.. 2배율로 하는 것이 훨씬 플랙시블 한 것 같다.
풀이
final int UP = 0, DOWN = 1, LEFT = 2, RIGHT = 3;
int dy[] = {-1, 1, 0, 0};
int dx[] = {0, 0, -1, 1};
class Node {
int y, x, cnt;
public Node(int y, int x, int cnt) {
this.y = y;
this.x = x;
this.cnt = cnt;
}
}
class Rectangle {
int y1, x1, y2, x2;
public Rectangle(int y1, int x1, int y2, int x2) {
this.y1 = y1;
this.x1 = x1;
this.y2 = y2;
this.x2 = x2;
}
public boolean isInner(int ny, int nx) {
return y1 < ny && y2 > ny && x1 < nx && x2 > nx;
}
}
public int solution(int[][] rectangle, int characterX, int characterY, int itemX, int itemY) {
Set<Integer>[][] path = new Set[51][51];
boolean[][] v = new boolean[51][51];
for(int i=0; i<51; i++){
for(int j=0; j<51; j++){
path[i][j]=new HashSet<>();
}
}
List<Rectangle> rects = new ArrayList<>();
for (int[] r : rectangle) {
int y1 = r[1];
int x1 = r[0];
int y2 = r[3];
int x2 = r[2];
// 시계
path[y1][x1].add(RIGHT);
path[y1][x2].add(DOWN);
path[y2][x2].add(RIGHT);
path[y2][x1].add(UP);
// 반시계
path[y1][x1].add(DOWN);
path[y1][x2].add(LEFT);
path[y2][x2].add(UP);
path[y2][x1].add(RIGHT);
for (int i = x1 + 1; i < x2; i++) {
path[y1][i].add(RIGHT);
path[y1][i].add(LEFT);
}
for (int i = y1 + 1; i < y2; i++) {
path[i][x2].add(DOWN);
path[i][x2].add(UP);
}
for (int i = x2 - 1; i > x1; i--) {
path[y2][i].add(LEFT);
path[y2][i].add(RIGHT);
}
for (int i = y2 - 1; i > y1; i--) {
path[i][x1].add(UP);
path[i][x1].add(DOWN);
}
rects.add(new Rectangle(y1, x1, y2, x2));
}
LinkedList<Node> q = new LinkedList<>();
q.offer(new Node(characterY, characterX, 0));
v[characterY][characterX] = true;
while (!q.isEmpty()) {
Node cur = q.poll();
System.out.println(cur.y + ", " + cur.x + " - " + cur.cnt);
if (cur.y == itemY && cur.x == itemX) {
return cur.cnt;
}
for (int dir : path[cur.y][cur.x]) {
int ny = dy[dir] + cur.y;
int nx = dx[dir] + cur.x;
if (v[ny][nx])
continue;
if (isInnerRects(ny, nx, rects))
continue;
v[ny][nx] = true;
q.offer(new Node(ny, nx, cur.cnt + 1));
}
}
return -1;
}
boolean isInnerRects(int ny, int nx, List<Rectangle> rects) {
for (Rectangle r : rects) {
if (r.isInner(ny, nx)) {
return true;
}
}
return false;
}
'Algorithm > 프로그래머스' 카테고리의 다른 글
| 프로그래머스 - N으로 표현 (0) | 2023.04.21 |
|---|---|
| 프로그래머스 - 퍼즐조각 맞추기 (0) | 2023.04.17 |
| 백준 - 무기공학 (0) | 2023.04.16 |
| 프로그래머스 - 미로탈출 명령어 (0) | 2023.04.15 |
| 프로그래머스 - 표 편집 (0) | 2023.04.12 |


댓글