2609번: 최대공약수와 최소공배수
첫째 줄에는 입력으로 주어진 두 수의 최대공약수를, 둘째 줄에는 입력으로 주어진 두 수의 최소 공배수를 출력한다.
www.acmicpc.net
유클리드 호제법은 2개의 자연수에 대한 최대공약수를 구하는 알고리즘이다.
호제법이란?
=> 두 수가 서로 상대방 수를 나누어서 최대공약수를 얻는 것이다.
2개의 자연수(또는 정식) a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다. 이 성질에 따라, b를 r로 나눈 나머지 r’를 구하고, 다시 r을 r’로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수이다.
최대공약수 GCD(Greatest Common Divisor)
최대공약수는 두 자연수의 공통된 약수 중 가장 큰 수를 의미한다.
ex) 72 와 30의 최대공약수는 6이다.
문제풀이
1) 두 수의 최대 공약수를 유클리드 호제법을 통하여 구한다.
2) 두 수 A, B를 곱한뒤 최대 공약수로 나눈 값을 최소 공배수로 출력한다.
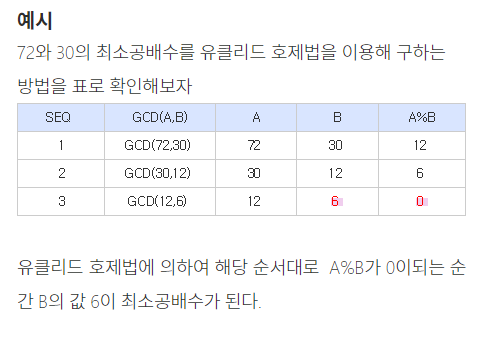
※ a>b보다 항상 커야 하므로 if 문으로 n>m을 구분하였다.
package Al_Study.기초수학;
import java.util.Scanner;
public class 최대공약수_최소공배수 {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int m=sc.nextInt();
int a;
if(n>m)
{
a=gcd(n,m);
System.out.println(a);
System.out.println(lcm(n,m,a));
}
else
{
a=gcd(m,n);
System.out.println(a);
System.out.println(lcm(m,n,a));
}
}
static int gcd(int a,int b)
{
while (b>0)
{
int tmp=a;
a=b;
b=tmp%b;
}
return a;
}
static int lcm(int a,int b,int gcd)
{
return (a*b)/gcd;
}
static void swap(int a,int b)
{
int temp=a;
a=b;
b=temp;
}
}
'Algorithm > AlgorihmFoundation' 카테고리의 다른 글
| MnimumSpanningTree (Kruskal+Disjoint_set(UnionFind) (0) | 2020.12.15 |
|---|---|
| Backtracking _N-Queen (0) | 2020.11.23 |
| Backtracking-N과 M (1) (0) | 2020.11.23 |


댓글