Graph
- 노드와 간선을 하나로 모아 놓은 자료구조.
- ex) 지도, 지하철, (최단거리),선수과목 ....
- 트리 또한 그래프라고 할 수 있다. 단, 사이클을 허용하지 않는다.
※ 그래프와 트리의 차이
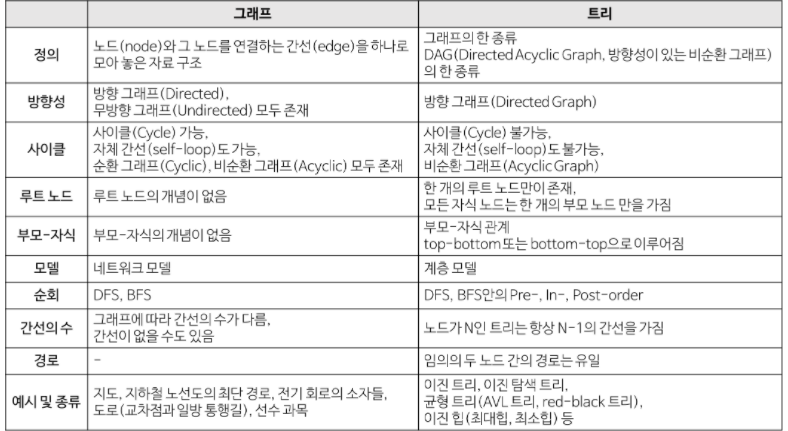
관련 용어 정의
| 정점 (vertax) |
점,위치 라는 개념.(node라고 부름) |
| 간선 (edge) |
점,위치 간의 관계, 노드를 연결하는 선(link ,branch 라고 함) |
| 인접 정점(adjacent vertax) | 간선에 의해 연결된 주변 점들. |
| 정점의 차수 (degree) |
무방향 그래프에서 하나의 정점에 인접한 정점의 수 ※ 무방향 그래프에 존재하는 정점의 모든 차수의 합= 그래프의 간선 수의 2배 |
| 진입 차수 (In- degree) |
한 정점을 기준으로 외부에서 들어오는 간선의 수 |
| 진출 차수 (out- degree) |
한 정점을 기준으로 외부로 향하는 간선의 수 |
| 경로 길이 (path length) |
경로를 구성하는 데 사용된 간선의 수 |
| 단순 경로 (simple path) |
경로 중에 반복되는 정점이 없는 경우 |
| 사이클 (cycle) |
단순 경로의 시작 정점과 종료 정점이 동일한 경우 |
그래프의 특징
- 네트워크 모델.
- 2개 이상의 경로가 가능(단방향,양방향)
- self loop가 가능하다.
- 계층형 모델이 아니므로 부모/자식 개념이 없다.
- 순환 / 비순환 그래프가 존재한다.
그래프의 종류
| 무방향 그래프 | ex) a-b a에서 b로 갈수도 있고 b에서 a로 갈 수 있다. |
| 방향 그래프 | ex) a->b a에서 b로만 갈수 있고 b에서 a로는 갈 수 없다. |
가중치 그래프와 부분 그래프
| 가중치 그래프 (weight graph) |
간선의 가중치 정보로 구성된 그래프(가중치는 거리 또는 시간, 노려의양 등이 될수 있다) |
| 비 가중치 그래프==부분 그래프 ( sub graph) |
모든 간선의 가중치가 동일한 그래프, 부분 집합과 유사한 개념이다. |
그래프 구현 방법
인접행렬 : 정방 행렬을 사용하는 방법.
해당하는 위치의 value 값을 물리적 논리적 위치가 같은 배열을 이용해 빠르게 접근 할 수 있어 O(1) 라는 시간복잡도를 갖는다. 하지만 정점의 개수가 많을 때 배열의 크기 또한 커지게 되므로 메모리 사용에 유의 해야 한다. Dense Graph를 표현할 때 적절하다.
인접 리스트 : 연결 리스트를 이용하는 방법.
물리적,논리적 위치가 같지 않아 어떤 점과 어떤 점이 연결되있는 것을 확인 할 때 찾는데 오래걸리는 단점이 있다. 왜냐하면 인접행렬은 arr[a][b]!=0 아니면 연결되있는 것으로 되있므로 찾기가 쉬운데 a리스트에 담긴 리스트를 모두 일일히 확인하면서 순회해야 하므로 오래걸리기 때문이다.
하지만 정점의 개수가 많을 때 사용해도 메모리 사용에 영향이 없다, 그러나 간선의 개수에 영향을 받는다.
Sparse graph를 표현하는데 적당한 방법이다.
그래프 탐색 방법
너비 우선 탐색(Breadth First Search)
- 한 정점과 연결된 인근의 점들을 순차적으로 방문하면서 탐색하는 방법이다.
- Queue를 사용한다.
- 첫 정점을 넣고 첫 정점을 뽑음과 동시에 인근에 존재하는 점들을 순회하고 방문한다.
- 트리 형식에서 같은 레벨의 탐색을 우선적으로 탐색하는 방법이다.
- Time Complexty : O(V+E)
- 최단 경로에 자주 쓰인다.
깊이 우선 탐색(Depth First Search)
- 한 정점에서 연결된 인접한 정점들 중 한 정점으로만 나아가는 방법으로 탐색하는 방법이다.
- Stack을 사용한다.
- 트리 형식에서 가장 높은 레벨로 나아가면서 탐색하는 방법이다.
- Time Complexty : O(V+E)
- 갓던 길을 되돌아 오는 상황의 미로찾기 처럼 구성된다.
※ 그래프 관련 알고리즘
- MST = 모든 정점을 최소의 거리로 이루어 질 수 있도록 하는 알고리즘이다.
- 단 사이클이 존재하지 않는다.
- Kruskal(O(ElogE)), Prim(O(ElogV))
- Dijksta = 한 정점을 기준으로 도달할 수 있는 최소거리를 만들어주는 알고리즘이다.( O(ElogV)


댓글