Tree
- 비선형 자료구조 이다.
- Hierachical 관계를 갖는다.(= 부모와 자식 관계를 갖는다)
- 트리는 DAG의 한 종류다( Directerd Acyclic Graphs 방향성 있는 비순환 그래프)
- 검색에 효율적인 구조를 갖는다.
※트리 관련 용어
- Node : 트리 구성 각 요소.
- Edge : 트리를 구성 하기 위한 노드 간 연결을 하는 선.
- Root Node : 트리 구조에서 가장 위에 있는 노드.
- Terminal Node(=Leaf Node) : 하위에 따른 노드가 연결되지 않은 노드.
- Internal Node : Terminal 노드를 제외한 모든 노드로 루프 노드를 포함한다.

+++
- 노드의 크기 : 자신을 포함한 모든 자손의 노드 개수
- 노드의 깊이 : 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수.
- 노드의 레벨 : 트리의 특정 깊이를 가지는 노드의 집합.
- 노드의 차수 : 각 노드가 지닌 가지의 수.
- 트리의 차수 : 트리의 최대 차수.
- 트리의 높이 : 루트에서 가장 깊숙히 있는 노드의 깊이.
트리의 조건
- 루트노드를 제외한 모든 노드는 단 하나의 부모 노드만을 가진다.
- 임의의 노드에서 다른 노드로 가는 경로(Path)는 유일하다.
- Cycle이 존재하지 않는다.
- 엣지를 하나 자르면 트리가 분리된다.
- Edge의 수는 Vertax-1이다.
트리의 종류
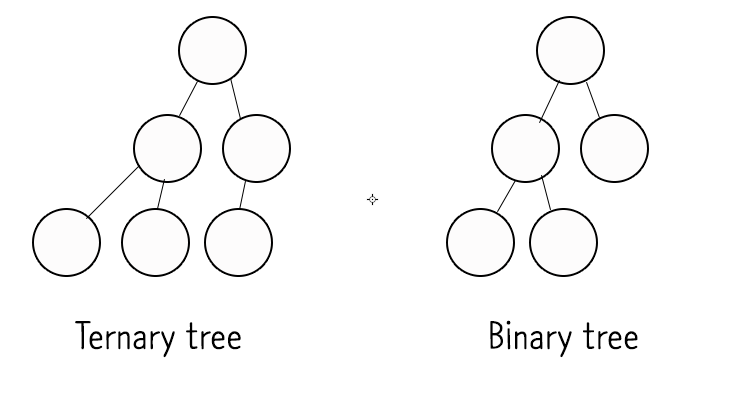
- 이진트리(Binary Tree)
- 부모 노드가 자식노드를 최대 2개씩만 갖고 있는 트리.
- 이진 검색 트리(BInary Search Tree)
- 노드들 간 대소관계를 고려한 트리.
- 이진 트리는 노드들 간 대소 관계를 고려하지 않음.
- 대소 관계 : 왼쪽 노드 < 부모 노드 < 오른쪽 노드

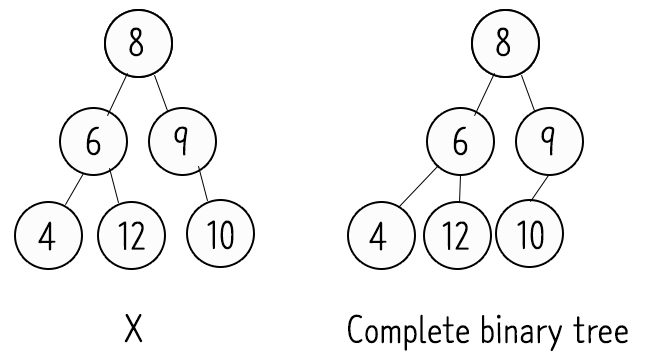
- 완전 이진 트리(CompleteBinaryTree)
- 마지막 레벨을 제외한 모든 서브트리의 레벨이 같아야 한다.
- 마지막 레벨은 왼쪽 부터 채워져 있어야 함.
- 배열로 표현이 가능.
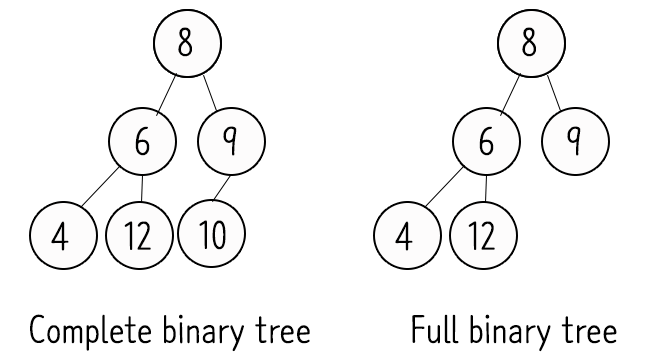
- 정 이진 트리(Full Binary Tree==Strictly Binary Tree)
- 자식을 하나만 가진 노드는 없어야 한다.
- 자식 노드가 아예 없거나, 최대 둘 뿐인 Tree.
- 포화 이진 트리(Perfect Binary Tree)
- 완벽한 피라미드 형태로, 빈 공간 없이 모든 노드가 2개의 자식을 갖고 있는 Tree.
- 레벨이 n 일떄 노드의 수는 2^n-1;

더보기
ratsgo.github.io/data%20structure&algorithm/2017/10/21/tree/
트리(tree)와 이진트리(binary tree) · ratsgo's blog
이번 글에서는 다양한 분야에서 널리 쓰이고 있는 자료구조인 트리(tree)와 트리의 일종인 이진트리(binary tree)에 대해 살펴보도록 하겠습니다. 힙 정렬이 뭔지 알아보려면 여러가지 개념을 먼저
ratsgo.github.io
gmlwjd9405.github.io/2018/08/12/data-structure-tree.html
[자료구조] 트리(Tree)란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
[자료구조] 트리(Tree) - 트리의 종류, 3가지 순회방법
아래의 유툽영상을 바탕으로 작성되었습니다. 좋은영상 감사합니다. Tree의 종류 : https://youtu.be/LnxEBW29DOw 0. 트리(tree)란? 즉 Array, LinkedList, Stack, Queue같이 선형구조가 아닌, 부모자식의 관..
it-and-life.tistory.com
'CS > DataStructure' 카테고리의 다른 글
| 정렬 (0) | 2021.07.19 |
|---|---|
| Hash (0) | 2021.04.12 |
| Heap (0) | 2021.03.30 |
| Stack and Queue (0) | 2021.03.30 |
| Array vs Linked List (0) | 2021.03.30 |


댓글