Hash Table
- ( key,value ) 로 데이터를 저장하는 자료구조 이다.
- 배열(버킷)을 사용하여 데이터를 저장하기 떄문에 빠른 검색 속도를 갖는다.
- ※배열은 물리적 위치와 논리적 위치가 동일하므로 빠르게 접근 가능하기 때문 avg_O (1).
- 하지만 문제는 인덱스로 저장되는 key값이 불규칙하다는 것이다.
- 특별한 알고리즘을 이용하여 저장할 데이터와 연관된 고유한 숫자(key)를 만들어 낸 뒤 이를 인덱스로 사용.
- 이 index를 활용해 값을 저장하거나 접근할 수 있고 실제 값이 저장되는 장소를 "버킷" 또는 "슬롯"이라고 한다.
- 특정 데이터가 저장되는 인덱스는 그 데이터 만의 고유한 위치이기 때문에, 삽입 연산 시 다른 데이터 사이에 끼어들거나 삭제 시에 다른 데이터로 채울 필요가 없으므로 연산에 대한 추가적인 비용이 없는 구조이다.
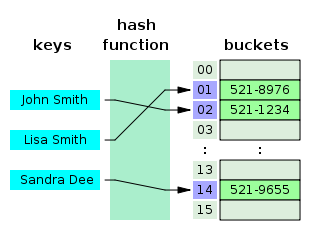
예를 들어 key가 String 값이라고 하면 "john Smith","521-1234" 쌍의 키 값 index=hash_function("jon")%16 연산을 통해 index를 계산하고 arr[index]="1" 계산하고 값을 저장한다. 이렇게 데이터를 찾을 때 함수를 단 1번만 수행하면 되므로 평균 시간복잡도는 O(1)이 된다.
※
- 평균 O(1)을 갖지만 충돌이 발생할 경우 최대 o(N)만큼의 시간복잡도가 증가한다.
- 테이블이 꽉 차 있는 경우 테이블의 확장을 고려해야 한다. 일정 개수가 차게 되면 동적으로 버킷의 개수를 두배로 늘린다 . 버킷의 개수가 0.75 정도를 가지면 확장을 한다.
- 70~80 %정도가 되면 충돌이 빈번하게 발생되어 성능이 저하되므로 여분의 공간 20~30% 있는 상태가 가장 좋다.
- 해시 테이블에서 자주 사용되는 데이터들을 Cache에 적용하면 효율을 높일 수 있다.
hash Funtion
- 해시 함수에서 고유한 인덱스 값을 설정하는 것이 가장 중요하다.
- 대표적인 해시함수는 4가지가 있다.
- Division Method
- 입력 값을 테이블의 크기로 나누어 계산한다. ( ref address= input % tabkeSize) 테이블의 크기를 소수로 정하고 2의 제곱수와 먼 값을 사용해야 효과가 좋다고 한다.
- Digit Folding
- key의 문자열을 아스키 코드로 바꾸고 각 문자 값을 합한 데이터를 테이블 내 주소로 사용하는 방법.
- Multiplication Method
- 숫자로 된 키 값(K) 와 0-1사이 실수 (A) , 2의 제곱수 m을 사용하는 방법
- H(K) = (K A mod 1) * m
- Universal Hashing
- 다수의 해시함수를 만들어 집합 H에 넣어두고 , 무작위로 해시함수를 선택해 해시값을 만드는 기법.
- Division Method
해시 함수의 충돌 전략
- 분리 연결법(Separate Chaining)
- 동일한 버킷의 데이터에 대해 자료구조를 활용하여 추가 메모리를 사용하여 다음 데이터의 주소를 저장하는 것.
- ※ 실제로 JAVA8의 hash 테이블은 Self- Balacing Binary Search Tree 자료구조를 사용해 Chaining방식을 구현하였다.
- 해시테이블의 확장이 필요없고 간단하게 구현이 가능하며 , 손쉽게 삭제할 수 있는 장점이 있다.
- 하지만 데이터의 수가 많아지면 chaining되는 데이터가 많아지며 그에 따라 캐시의 효율성이 감소한다는 단점이 있다.
- 동일한 버킷의 데이터에 대해 자료구조를 활용하여 추가 메모리를 사용하여 다음 데이터의 주소를 저장하는 것.
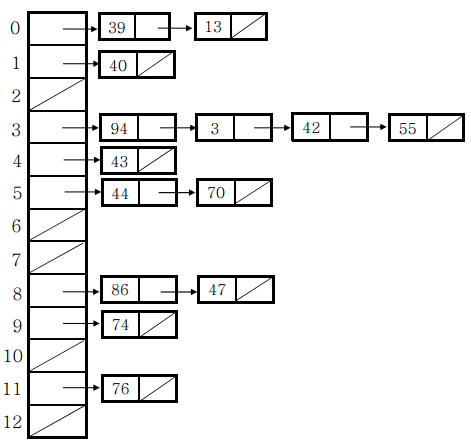
- _
- Tree를 사용하는 방식 (Red Black Tree)
- 리스트와 트리를 선택 할 기준은 해시 버킷에 할당된 key value쌍의 개수이다. 데이터의 개수가 적다면 링크드가 좋다.
- 트리는 기본적으로 메모리 사용량이 많다.
- 하지만 리스트의 탐색 효율보다 트리의 탐색 효율이 더 좋기 때문에 key value 쌍의 개수가 많을 때는 트리 형식을 택한다.
- 트리 방식은 메모리는 링크드보마 많이 사용하지만 많은 데이터의 검색 효율에서는 뛰어나다.
- 개방 주소법(Open Addressing)
- 추가적인 메모리를 사용하는 방식의 Chaining 과는 다르게 해쉬 테이블의 공간을 활용하는 방법이다.
- Linear Probing
- 현재 버킷 index로 부터 고정폭 만큼씩 이동하여 차례대로 검색해 비어 있는 버킷에 데이터를 저장한다.
- Quadratic Probing
- 해시의 저장순서 폭을 제곱으로 저장하는 방식.
- 처음 충돌이 발생할 경우 1만큼 , 또 충돌이 날 경우 2^1 그다음 2^2......
- Double Hashing Probing
- 해시 된 값을 한 번더 해싱하여 규칙성을 없애버리는 방식.
- 해시된 값을 한 번더 적용하므로 새로운 주소로 할당한다 그래서 다른 방법들 보다 연산을 많이한다.
- Linear Probing
- 추가적인 메모리를 사용하는 방식의 Chaining 과는 다르게 해쉬 테이블의 공간을 활용하는 방법이다.
'CS > DataStructure' 카테고리의 다른 글
| 그래프 (0) | 2021.07.30 |
|---|---|
| 정렬 (0) | 2021.07.19 |
| Heap (0) | 2021.03.30 |
| Tree (0) | 2021.03.30 |
| Stack and Queue (0) | 2021.03.30 |


댓글